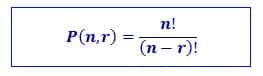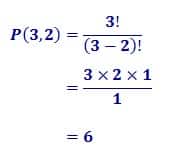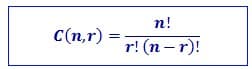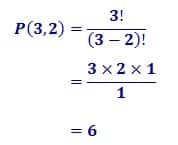UAS Matematika Diskrit 1 Kampus Milenial ITBI Semester 1 (SATU)

Nama       : IRNA MARLIANA SIREGAR 

Kelas        : Pagi

Jurusan   : Informatika

 

SOAL
1. Tentukan apakah graf dibawah ini memiliki sirkuit Hamilton. Jika tidak, berikan alasannya. Jika memiliki, carilah sirkuit Hamilton tersebut.

 

 

 

 

 2. Tentukan apakah graf dibawah ini isomorfis? Jika ya atau tidak berikan alasannya

 

 

 

3. Misalkan A={2,3,4} dan B={6,8,10}. Didefenisikan relasi biner R dari A ke B sebagai berikut: untuk semua (x,y) elemen A x B (x,y) elemen R jika dan hanya jika x|y ( x habis membagi y).
a. Tulis R sebagai pasangan berurut.
b. Buatlah R dalam bentuk graf.

4. MisalkanW = {1, 2, 3, 4}. Perhatikan relasi-relasi dalam W berikut ini : R1 = {(1,1), (1,2)}, R2 = {(1,2), (2,4)}, R3 = {(1,1), (2,2), (3,3)} Selidiki apakah masing-masing relasi diatas bersifat Refleksif, Simetris, Transitif.

5. Hitunglah P(8,5) dan C(12,6)!

6. Berapa banyak plat nomor kendaraan yang bisa dibuat dari 2 huruf dan diikuti dengan 4 angka ?

7. Suatu komite yang beranggotakan paling sedikit 5 orang akan dipilih dari 9 calon yang ada. Berapa
maacaam komite yang dapat dibuat ?

8. Suatu kode akses computer terdiri dari 3 huruf dengan mengizinkan perulangan. Berapa banyak di
antara kode-kode tersebut memuat perulangan huruf.

9. Buktikan deret dibawah ini dengan menggunakan induksi matematika dimana n >1 

 

 

10. Tuliskan pengaruh Algoritma terhadap komputasi atau program yg kita buat?

 

Jawaban

1. Iya, graf tersebut memiliki sirkuit hamilton, yaitu : 

 

(a, b, c, d, e)  

 

 

 

 

  

 

2. Iya, Graf tersebut adalah Graf isomorfis karena: 

• Mempunyai jumlah simpul yang sama
• Mempunyai jumlah sisi yang sama 
• Mempunyaj jumlah simpul yang sama berderajat tertentu

3. Dik : A={2,3,4} B ={6,8,10}

Dit : a). R sebagai pasangan berurut b). R dalam bentuk Graf

Jawab :

a). R= A={2,3,4} B={6,8,10}

AxB ={(2,6),(2,8),(2,10),(3,6),(3,8),(3,10),(4,6),(4,8),(4,10)}

b). 

4. R1={(1,1),(1,2)}=relasi bersifat refleksif

R2={(1,2),(2,4)}= tidak bersifat refleksif,simetris,dan transitif

R3={(1,1),(2,2)}= rellasj bersifat refleksif

5. 

6. Kemungkinan huruf yang dipakai yaitu 26 (abjad),

kemungkinan angka yang dipakai ada 10 angka (0-9)

Banyak plat nomor yang nomor yang dapat disusun: 26x25x10x9x8x7=3.276.000 plat

7. 

8. 3 huruf boleh berulang =1,2,3 maka banyaknya cara: 3x3x3 =27

9.

10. Algoritma pemprograman mungkin sudah tak asing lagi bagi anda yang bekerja di suatu perusahaan dan bekerja di bidang pemprograman. Suatu program sudah tentu sangat dibutuhkan kehadirannya terutama pada suatu suatu perusahaan. Penggunaan program untuk suatu sistem komputasi memang sudah menjadi hal hal yang biasa dimasa seperti sekarang ini. Bahkan penggunaan berbagai program selalu dianjurkan karena dengan adanya program maka segala hal bisa dilakukan dengan lebih mudah. Penggunaan program juga bisa dilakukan dengan lebih praktis sehingga bisa mempermudah pekerjaan anda dan memberikan hasil yang lebih maksimal.

Mandiri 6 - Matematika Diskrit 1 Kampus Milenial ITBI Semester 1 (SATU)

Nama       : IRNA MARLIANA SIREGAR 

Kelas        : Pagi

Jurusan   : Informatika

 

SOAL:

1. Jelaskan hubungan antara algoritma dan bahasa pemrograman komputer !   

2. Apakah perbedaan antara algoritma dan logika?                                                                   

3. Jelaskan apa pentingnya mempelajari kompleksitas suatu algoritma tertentu !                     

4. Jelaskan pengertian flowchart ! 

5. Soal Kombinatorial   

1. Jelaskan perbedaan antar permutasi dan kombinasi kemudian buat masing-masing 1 contoh dan penyelesaian! 
2. Berapakah jumlah kemungkinan membentuk 4 angka dari 6 angka berikut: {1,2,3,4,5,6} jika tidak boleh ada pengulangan angka (permutasi)? 

 Jawaban

1.  hubungan antara algoritma dan bahasa pemrograman komputer, yaitu : 

• Algoritma baru efektif jika dilaksanakan oleh sebuah pemroses (processor).
• Pemroses itu bisa manusia, komputer, robot, mesin, dsb. 
• Supaya komputer mengerti instruksi yang dibacanya, maka instruksi tersebut harus ditulis dalam bahasa yang dipahami oleh komputer. 
• Algoritma yang ditulis dalam bahasa komputer disebut program
  
• Bahasa komputer yang digunakan untuk menulis program disebut bahasa pemrograman, sedangkan orang yang menulis program computer dinamakan pemrogram (programmer).
• Kegiatan mulai dari mendesain hingga menulis program disebut pemrograman. 

 2.  Logika dan Algoritma merupakan kesatuan yang tidak dapat dipisahkan karena keduanya saling berkaitan. Logika adalah bentuk penalaran atau pemikiran, sedangkan Algoritma adalah suatu urutan dari barisan langkah-langkah atau instruksi untuk menyelesaikan suatu masalah. Pengertian logika dan algoritma adalah suatu urutan dari beberapa langkah yang logis guna menyelesaikan masalah.

3. pentingnya mempelajari kompleksitas suatu algoritma tertentu, yaitu :

• Algoritma membantu kita memahami skalabilitas program kita.
• Performa terkadang menjadi pembeda antara yang mungkin dilakukan dan yang tidak mungkin dilakukan.
• Analisa algoritma memberi gambaran informasi tentang 'perilaku program' kita.
• mempelajari bagaimana menerapkan algoritma yang baik untuk kasus tertentu membedakan profesi system analyst dan programmer.

4.  Flowchart merupakan sebuah bagian dengan simbol (sandi) tertentu yang menjelaskan dan menggambarkan langkah-langkah proses secara mendetail, dan hubungan antara proses (metode) dengan proses lainnya pada suatu program.

 

 5.Kombinator :  

1. Permutasi adalah banyaknya cara untuk membuat susunan dengan jumlah pada suatu anggota tertentu dari anggota-anggota suatu himpunan. 

Rumus Permutasi, misal diketahui himpunan memiliki anggota sejumlah n, maka susunan terurut yang terdiri dari r buah anggota dinamakan permutasi r dari n, ditulis sebagai P(n,r) dimana r lebih kecil atau sama dengan n. Rumus permutasi adalah sebagai berikut.

 

Jika r = n, Maka P (n,n) = n! (ingat 0!=1)

contoh : untuk menghitung banyaknya cara menyusun urutan dua huruf dari huruf-huruf a, b, c adalah sebagai berikut.

 

Kombinasi adalah banyaknya cara memilih anggota pada jumlah tertentu dari dari anggota-anggota suatu himpunan. Atau dengan kalimat lain kombinasi yaitu banyaknya cara membuat himpunan bagian dengan jumlah anggota tertentu dari anggota-anggota suatu himpunan.

Rumus Kombinasi, misal diketahui suatu himpunan mempunyai anggota sejumlah n, maka pemilihan r buah anggota dinamakan kombinasi r dari n, dan ditulis sebagai C (n,r) dimana r lebih kecil atau sama dengan n.

Rumus kombinasi adalah sebagai berikut

 

Contoh : menghitung banyaknya tata cara menyusun urutan dua huruf dari huruf-huruf a, b, c
 

Perbedaan Permutasi dan Kombinasi

Setelah mengetahui dua rumus tentang permutasi dan kombinasi, hal yang tak kalah penting yaitu membedakan permasalahan yang termasuk dalam permutasi ataupun kombinasi. Permasalahan yang selalu muncul berupa soal cerita dan dituntut agar bisa membedakan masalah tersebut termasuk kedalam permutasi ataupun kombinasi. Hingga, tak terjadi kesalahan dalam menggunakan rumus untuk menyelesaikan masalah dalam hal tersebut.

Permasalahan pertama : permasalahan permutasi
Susunan panitia yang terdiri atas ketua, sekretaris, wakil ketua dan bendahara akan dibentuk untuk mensukseskan suebuah acara. Susunan panitia tersebut akan dipilih dari 10 orang yang terpilih berdasarkan kriteria yang sudah ditentukan. Berapakah banyaknya susunan panitia yang bisa dibentuk?

Penjelasan: susunan urutan menjadi sebuah bagian yang perlu diperhatikan. Kedudukan ketua untuk orang pertama tentu akan berbeda dengan ketua yang ditempati pada orang ke tiga. Begitu juga dengan kududukan untuk posisi yang lainnya.

Permasalahan ke dua: permasalahan kombinasi
Enam buah buku akan dipilih dari lima buku materi Matematika, tiga buku materi Fisika, dan empat buah buku materi Kimia untuk disumbangkan ke sekolah anak jalanan.
Berapakah banyaknya cara yang bisa dilakukan untuk memilih enam buku tersebut?

Penjelasan: pemilihan buku pada urutan pertama dan kedua misalnya yaitu buku Matematika pertama dan pada buku Matematika ke dua, keduanya merupakan buku materi Matematika. Hingga, urutan tidak terlalu dipehatikan. Pada intinya, rumus permutasi dipakai untuk permasalahan yang memperhatikan urutan. Sedangkan kombinasi dipakai untuk menyelesaikan permasalahan yang tidak memperhatikan urutan.

contoh soal : 3 orang anak akan duduk bersama di sebuah bangku yang panjang. Ada berapakah cara mereka duduk bersama pada bangku tersebut?
Jawaban:
Ketiga anak akan duduk bersama, maka dipakai rumus permutasi P(3,3)
P(3,3) = 3 = 2x2x1 = 6
Maka ketiga anak tersebut bisa duduk bersama dengan 6 cara

 

2. Berapakah jumlah kemungkinan membentuk 4 angka dari 6 angka berikut: {1,2,3,4,5,6} jika tidak boleh ada pengulangan angka (permutasi)?

penyelesaian : dengan kaidah perkalian : (6),(5),(4) = 720 buah 

dengan rumus permutasi : P (6,4) = 6!/(6-4)! = 720